The curious case of the Weierstrass function

it's a function which is continous and nowhere differentiable

Jan 12, 2024

“In Some ways, fractal geometry is a rebellion against calculus.”

~ Grant Sanderson

One of the many theorems of calculus states that for a function differentiability implies continuity, that is if a function is differentiable everywhere then it’s also continuous everywhere.

A natural question is to wonder whether the converse is true? That is whether continuity implies differentiability. We as students come to learn that it’s not true, one of the many counterexamples is of the function |x| which is continuous at x=0 but not differentiable at that point. This seems reasonable enough, in fact it can be proven that when lines of different slopes meet they would create a point of discontinuity. But there is an interesting observation, let’s take our previous example f(x) = |x|, here we can see that there is only one point which is not differentiable. So although the converse of the previous theorem is objectively incorrect, some may try to salvage the converse by accounting for the finite number of points of non differentiability or excluding these points in some arbitrary definition. Afterall, there are infinite number points which are indeed differentiable, compared to the finite number of points of discontinuity, or a single point of discontinuity in the case of f(x)=|x|

This motivates the construction of a function which is continuous but nowhere differentiable. Such a function would be the quintessential counterexample of the aforementioned proposed theorem. It’s hard to imagine such a function, one may think of creating a function which oscillates quickly, a kind of zig-zag function. Which could look something like this:

\(f(x)=\frac{1-(-1)^{\lfloor ax\rfloor}}{2}+(-1)^{\lfloor ax\rfloor}(ax-\lfloor ax\rfloor)\)

Which when graphed for a=1 looks like this:

We can then increase the frequency(a) of the wave which for the value a=10 looks like this:

Hence it’s evident that for each such “zig-zag” there will be a point of non differentiability. Hence in our initial approach we have created a function which has infinite points of discontinuity. We could imagine that as the limit of the frequency value a reaches infinity, all points become points of non differentiability.

The limiting case would look something like this:

But this approach has major flaws.

For the finite values of frequency a there are still infinite number of points which are continuous and differentiable. And for the limiting value a tending to infinity, our relation is no longer a function!

The main problem with our approach was that we require that the frequency of the waves approach infinity, this result in the slope of the lines being infinite but that makes it so that the limiting “function” is no longer a function. This is evident in graphical representation of such a function but a crude argument is to see how the frequency is multiplied to x in the function which means that if you could take the derivative ( you can’t because it’s non differentiable but that’s why this is a crude argument) the frequency would come out of due to the chain rule which then tends to infinity which is a problem.

If the frequency is finite then after zooming sufficiently enough we would end up with parts of the function looking like straight lines in a definite interval which leads to infinite points of differentiability.

So it may seem impossible to construct a function which is continuous and nowhere differentiable but there is a way! Much like how it may seem that objects with infinite perimeter but finite area don’t exist, such objects do in fact exist. This is achieved with the help of fractals!

Fractals geometry consists of objects with non natural number dimensions… for instance the fractal corresponding to the coastline of Great Britain has the approximate dimension of 1.21 This is also the reason behind the coastline paradox! There is a very convincing way to define non natural number dimensions, further readings for the same is provided in the description

To summarise, fractals are strange objects which need not have a self referential pattern. Their characteristic property is that they don’t have any sense of length like 1D objects or area like 2D objects. This notion of length in 1D, area in 2D or volume in 3d is characterised by a mathematical object called the ‘measure’ which could be thought of something analogous to the mass of the object.

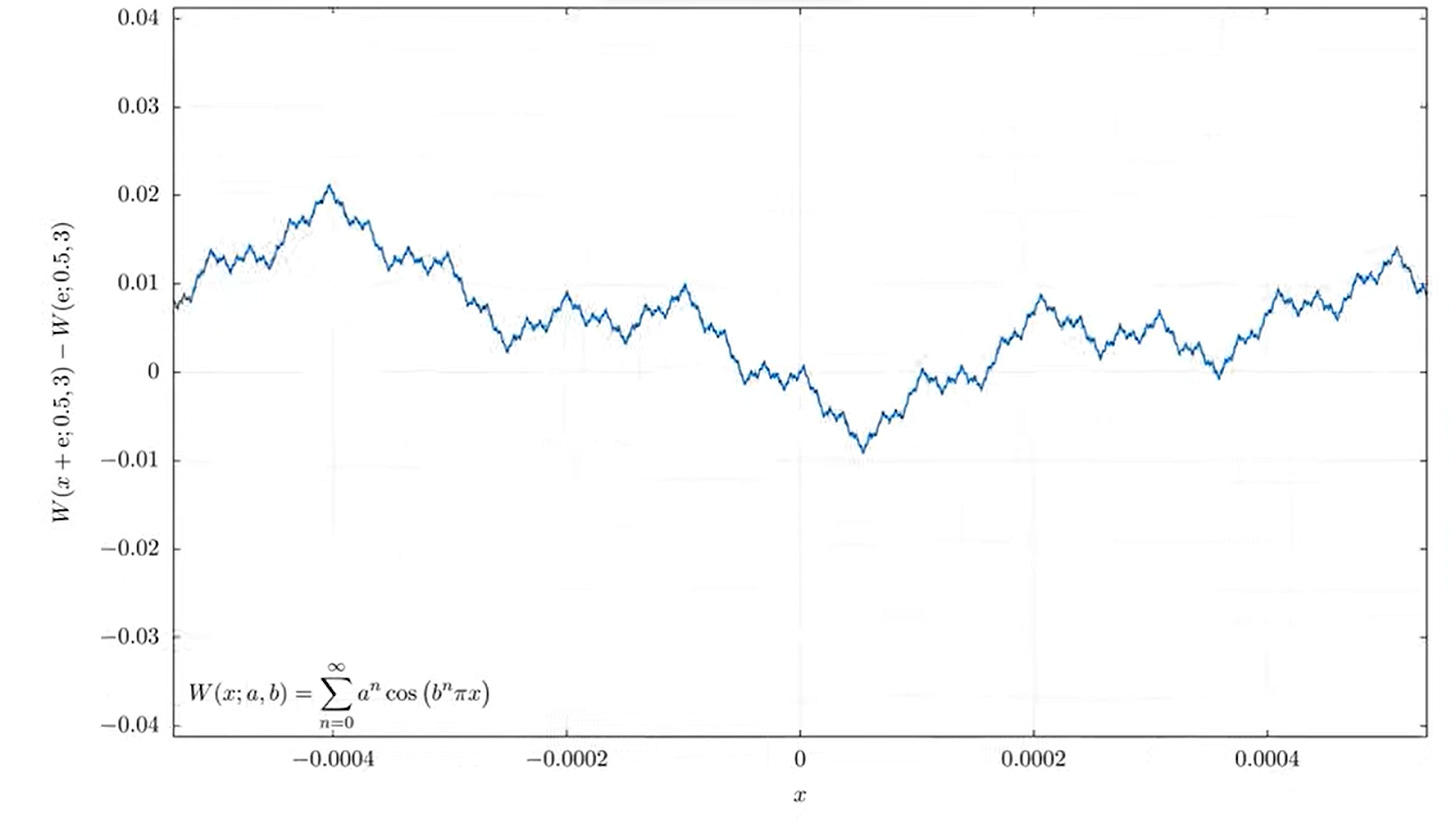
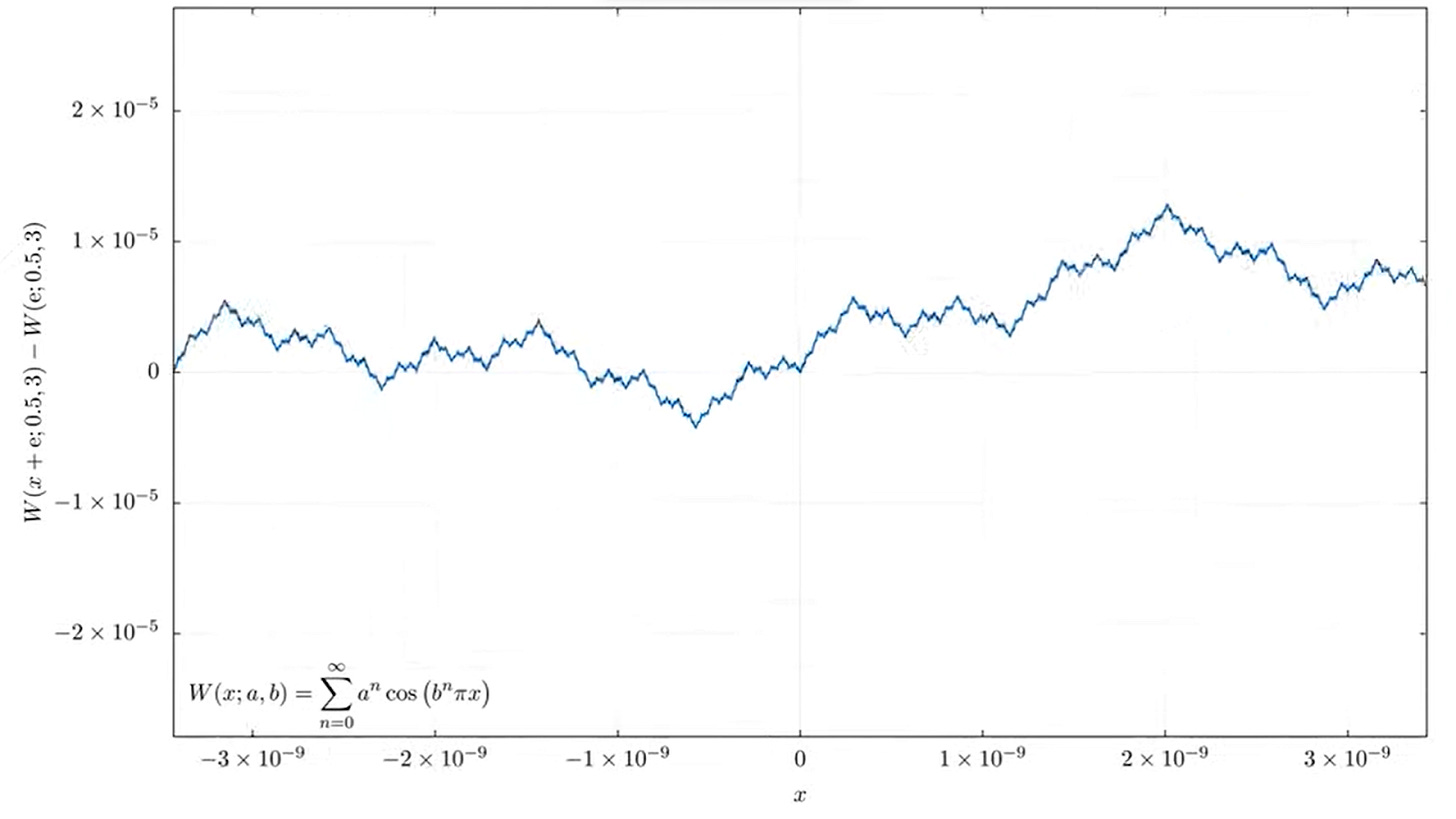
For our purposes the important part is that when dealing with fractal geometry there is no sense of length i.e. a fractal pattern can be “infinitely zoomed into”. Although there is no requirement that the pattern should be self referential ( self referential pattern forming fractals are only a subset of all fractals). Basically if there exists a fractal pattern which consists of lines of different slope meeting together, the more you zoom in, the more you’ll see similar( not necessarily the exact same) patterns, thus you’ll never find a region in a domain which consists purely of a straight line, thus you’ll never find a region which contains a point of differentiability. Hence if we find such a function with such properties that function will be continous and nowhere differentiable. Such a function was given by Weierstrass, who is also known as the father of modern analysis, which was:

\(f(x)=\sum_{n=0}^{\infty} a^n \cos \left(b^n \pi x\right)\)

Where 0<a<1 and b is a positive odd integer abiding the following constraint:

\(a b>1+\frac{3}{2} \pi\)

The function at a point is defined as the value which the infinite sum approaches… Some striking characteristics to look at is as n tends to infinity, the frequency of our cos function tends to infinity as well which is similar to our initial approach, but here the first term a^n tends to 0 (as 0<a<1) which in a way tames our infinity that is the limiting value exists . Also here our waves consist of cosine waves which are not straight lines, this is taken care of by a infinite sum which defines a fractal pattern consisting of straight lines, this is similar to a fourier series but is a bit different ( the frequency terms increases exponentially). These are crude but simplified arguments, resources for a more rigorous proof is provided in the Description.

The functions looks like this: